I. Introduction
Taking into account the simultaneity of the timing of
marriage, the fertility, and participation decisions is one of the principal
challenges in modeling female labor market behavior. Delayed marriage, and declining fertility in the MENA region in
general, and in Morocco, in particular, can potentially translate into
significant increases in female participation in market work. An accurate assessment of the impact of
these demographic changes on labor market behavior requires the specification
of structural models, that can disentangle the effect of fertilty and and the
timing of marriage on participation,from the impact of particpation on these
two sets of decisions.
The economic literature on the female particpation in the
labor force is quite extensive.
(Killingsworth 1983, Heckman et MaCurdy 1986, Killingsworth and Heckman
1986, Blundell 1990 and Browning 1992).
Studies focusing on the United States have shown that participation in
paid work is strongly related to age at marriage and fertility. In fact, fertility in the United States has
declined considerably in the 1960s (National Center for Health Statistics 1991)
in part due to the delay in marriage
(Rodgers and Thornton 1985, Espenshade 1985, Bianchi and Spain 1986)
and, in part, due to the reduction in the number of births per woman (Heckman
and Willis 1977).
Although many
early studies of female labor supply simply introduced the number and age of
children in the home as exogenous regressors in participation equations (Mincer
1962, Heckman 1974, Heckman and MaCurdy 1980), the recent literature has
insisted that these variables are potentially endogenous and can therefore
result in biased estimates(Schultz 1978, Dooley 1982, Moffit 1984, Hotz and
Miller 1988, Nakamura and Nakamura 1985, 1992). Mroz (1987) tested the sensitivity of the parameters of the labor
supply equation of married women with respect to a number of assumptions
including the exogeneity of the fertility decision, as captured by number of
childen in two age categories. He could
not reject the exogeneity of fertility in the case of hours of work. Xie (19970 conducted an exogeneity test for
both the particpation and hours of work equations using the generalized
residual method and rejected exogeneity in the particupatio decision, but could
not reject it for hours of work.
Some authors attempted to address the endogeneity of
fertility in the participation decision by adopting an instrumental variable
methodology, whereby auxiliary equations are estimated for number of children
and predicted values are subsitituted for the original child (Nakamura and
Nakamura 1992). The main challenge in
doing this has been to identify instruments that influence the fertility
decision without also affecting the particpation decision directly. In searching for suitable instruments for
fertility, researchers have looked for sources of unplanned births (like the presence
of twins) (Rosenzweig and Wolpin 1980) and to the availability and cost of
contraceptive technology (Rosenzweig and Schultz 1985). Previous work on female participation and
sector choice in the MENA region either assumes that the number of children a
woman has is exogenous to her participation or sector choice decision (Assaad
and El-Hamidi 2001, 2002, El Aynaoui 1997) or simply leaves that information
out altogether (Tunali and Baslevent 2001; Tansel
1994, 1996, 1999; Dayioglu 1999), essentially estimating a reduced form
model.
The timing of marriage is almost always left out as a
determinant of participation. The usual
practice in the female labor supply literature is to include marital status as
a set of exogenous dummy variables or
to limit the estimation of the participation or labor supply function to
married women. However the exogeneity
of marital status can also be called into question since particiption in the
workforce prior to marriage can allow women to delay marriage. In a structural framework, the timing of
marriage is also a crucial determinant of fertility, but may also be endogenous
to that decision.
Finally there is the issue of how participation itself is
modeled. The recent literature on
developing countries stresses the different forms of market work that women can
engage in and how each of these forms can have different implications for women
ability to combine market work and child care (Hill 1983, 1989, Tiefenthaler
1994, Assaad and El-Hamidi 2001). In
particular, self-employment can allow women to generate income while
simultaneously caring for their chidren.
Even within wage employment, public sector employment often involves
shorter hours than employment in the private sector and often provides child
care services that make it more compatible with child rearing.
Our paper attempts to address these various issues by
estimiating a structural model that takes into account the endogeneity of
fertility and the timing of marriage to the participation decision and by modeling
participation as a polychotomous variable that distinguishes between different
participation states. Since there is
little heterogeneity in the kinds of economic activities that rural women in
Morocco engage in, we focus our attention on urban women between the ages of 15
and 54. The rest of the paper is
organized as follows: section 2 discusses the methodolgy used in the
econometric estimation, section 3
discusses the sources of data and the characteristics of the sample we use,
section 4 presents our results, and section 5 concludes.
2. Methodology
The procedure we adopt in our empirical work consists of
three stages. The first stage consists
of estimating an equation for the age at first marriage using a parametric
duration model that takes into account that the dependent variable is censored
for the unmarried women in our sample.
We use this model to predict the age at first marriage for use in
modeling fertility and the probability of marriage for use in modeling
participation. The second stage
consists of estimating the determinants of the number of children born alive
and the number of children under seven years of age for married women using a
count data model. We use these
estimates to predict the number of children under seven and the number of
children seven and over, as the difference between the predicted total number
of children and the predicted number of children under seven. The final stage consists of estimating a
nested logit model of participation for all women that accounts for the
endogeneity of marital status and the number of children under seven and seven
and over [1].
The main challenge in this estimating procedure is to find
appropriate instruments for the endogenous regressors. In the case of the timing of marriage, we
use information from the mortality module of the survey on the total number of
married sisters a women has. This
variable is unlikely to directly affect either the fertility or participation
decisions, but is likely to affect the timing of marriage on the theory that
parents with many daughters will prefer to marry them off early. In the case of fertility, we obtain
estimates of average contraceptive use by age at the provincial level from the
Moroccan Demographic Health Survey of 1992.
These can as indicators of the availablity of family planning services
in the vicinity of where the woman lives, and are, therefore, appropriate
instruments for fertility.
First Stage: Estimation of the Timing and Probability of Marriage
The objective here is to predict the median age at first marriage for a woman of given characteristics for use as a regressor in the models for number of children and the probability of marriage for use as a determinant of the participation decision. In estimating the age at first marriage, we use a parametric duration model to account for the fact that the dependent variable is right censored for the unmarried women in the sample. Because the hazard of marrying is likely to first increase sharply after age 15, the legal age of marriage in Morocco, and then decrease gradually with age after the mid twenties, we adopt a generalized Gamma distribution, which allows for such a shape (See Figure 1).
Besides the number of married sisters a woman has, other explanatory variables for the age at first marriage include age cohort (in 5-year age categories), the woman’s education level, the education and work status of the parents, and region of residence. The woman’s own education variable had to be carefully specified so that it would not be affected by the timing of marriage. We have therefore specified educational attainment into three categories: no schooling (the reference category), some primary (six or fewer years of schooling) and primary and above (more than 6 years of schooling). The decision to continue schooling beyond six years, which is usually done around age 12, is not likely to be affected by when a woman is to be married.
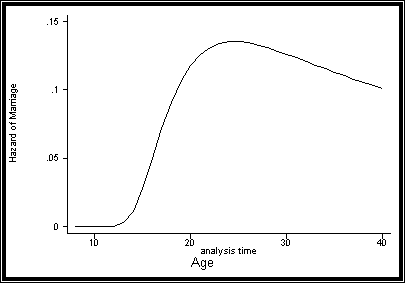
· Figure 1 : Hazard Function for the Timing of Marriage using a
Generalized Gamma Distribution
Analysis time in our model is a woman's age, with the earliest observed entry time being 7, the earliest age at marriage in the sample. The median age at first marriage is calculated as the time, t, at which the survival function, S(t), is equal to 0.5. The predicted probability of marriage is equal to 1-S(t), where t is a woman's actual age. The survival function under the Gamma parametrization is given by:
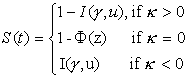
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() is the standard normal cumulative distribution function, and
is the standard normal cumulative distribution function, and ![]() is the incomplete
gamma function.
is the incomplete
gamma function. ![]() is the Gamma
parametrization shape parameter and
is the Gamma
parametrization shape parameter and ![]() is the scale parameter.
The model is implemented by parametrizing
is the scale parameter.
The model is implemented by parametrizing ![]() and treating
and treating ![]() and
and ![]() as ancillary
parameters to be estimated from the
data [2].
as ancillary
parameters to be estimated from the
data [2].
Second Stage: The Fertility
Decision
Because the age of the children present in the household
matters for the participation decision, we carry out estimates of both the
total number of children born alive as well as the number of children under
seven years of age for all ever married women in the sample [3]. In both cases we use the prediced age at
first marriage, obtained from the first stage, as a regressor.
To account for the fact that the number of children is not
a normally distributed continuous variables, it is preferrable to use a count
data model rather than OLS. We opt for
a negative binomial model, which is a count data distribution, which allows for
greater variation than a true Poission distribution. In the case of number of children under seven, the relevant
statistical tests show that the negative binomial model reduces to a Poisson
model, which we use to maximize efficiency.
As mentioned above the instrumental variables used in this
set of regressions are based on age-specific contraceptive use in the province
of residence, which is an indicator of access to family planning methdods and
general awareness of these methods. For
each of the 32 provinces represented
in the sample, we use data from the 1992 Moroccan Demographic Health Survey to
calculate mean use rates for different age cohorts of women for modern and
traditional contraception methods. We
thus produce a set of 14 instrumental variables (7 age groups by two types of
methods). Other explanatory variables
include the woman’s age and age squared, her level of education, the presence
of other adult women in the household, her parents’ education, and region. The model for children under seven has an
identical specification.
An additional set of instruments that could be used is the
presence of unplanned births, as indicated by having twins in the first
pregnancy (Rosenzweig and Wolpin, 1980).
In our case, the number of women having twins proved to be very small
and the rank of the twins in the order of births was other than the first pregancy
in over half the cases. Moreover, introducing
this variable would limit the sample to women who have had at least one
pregnancy, which would eliminate many
married women in our sample.
We use the estimates from the two fertility regressions to
predict the number of children born alive and the number of children under
seven for both married and unmarried women.
The predicted number of children who are seven and older is calculated
as the difference between these two predictions.
Before we can introduce the predicted number of children
in the two age groups into the third stage of our analysis – the participation
stage -- we need to deal with the fact
that our fertility estimates are conditional on being married, and marriage is
endogenously determined in our model.
We obtain estimate of the number of children that are unconditional on marriage by multiplying
the predicted probability of marriage obtained in the first stage with the
predicted number of children in the two age groups obtained in the second
stage.
Third Stage: The Participation
Decision
As discussed above, the forms of participation in economic
activity in the Moroccan context differ considerably in their implication for
combining household responsibilities, and especially child rearing, with market
work. Accordingly we distinguish
between five possible participation states, namely domestic work only
(non-participation), non-wage market work (which includes self-employment and
unpaid family labor), public wage work, private wage work, and unemployment. Although the multinomial logit specification
is often used for such a polychotomous dependent variable, this specification
suffers from the need to make the independence of irrelevant alternatives (IIA)
assumption. This assumption results
from the maintained assumption that the disturbances associated with the
utility derived from each option are independent and homoscedastic. One way to relax the IIA assumption is to
group the orginal alternatives into subgroups and allow the variances to differ
across the groups while maintaning the IIA assumption within the groups. This defines the nested logit model (Greene,
2000).
As shown in Figure 2, suppose that the particpation
decision can be subdivided into a three-level choice problem. The first level consists of the decision of
whether or not to engage in any kind of market work. The second level is a choice between wage and non-wage work for
those who decide to participate in market work and leaves the non-participants
as they are. The third level
distinguishes between public and private work and unemployment, for those who
select wage work, leaving the other branches unchanged [4]. Under the nested logit model, the IIA
assumption is maintained within the alternatives of each decision, but can be
relaxed across decisions.
1st level 2nd level 3rd level3
![]()
![]() Inactive Inactive Inactive
Inactive Inactive Inactive
![]()
![]()
![]() Active Non wage earner . Non wage earner
Active Non wage earner . Non wage earner
Wage earner Private
sector
Public sectoré
CUnemploymente
· Figure 2: Decision Tree for the Nested Logit Participation Model
Suppose that each alternative at the third level is associated with a level of utility given by:
![]() (1)
(1)
where Zj ,Yij , and Xijk ,and are vectors of explanatory variables specific to the first, second and third level choices, respectively and ei , eij , eijk are independent and identically distributed error terms with Weibull distribution [5]. The probability that an individual will choose alternative ijk in the third stage is given by:
![]() (2)
(2)
where the conditional probability ![]() will depend only on the parameter vector
will depend only on the parameter vector ![]() .
.
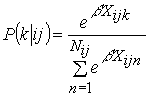 (3)
(3)
Define the inclusive value for the second level options j as:
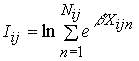
so that the second level
conditional probabilities ![]() are given by:
are given by:
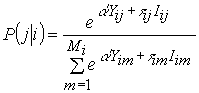 (4)
(4)
Similarly define the inclusive value for the first level options i as follows:
![]()
yielding the following unconditional first level probability P(i):
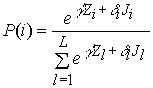 (5)
(5)
By substituting equations (3), (4) and (5) into equation (2), we obtain an expression of how the probability of each level-3 alternative depends on the explanatory variables and the model parameters. The nested logit model can be estimated by full information maximum likelihood estimation, where the log-likelihood function is given by:
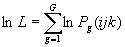 where g indexes
individuals in the sample.
where g indexes
individuals in the sample.
3. Data and Descriptive Statistics
Our main source of data from this study is the Moroccan Living Standards Measurement Study (LSMS), which was carried out in 1990-91. The overall sample for this household survey consists of 3,323 households, containing 19,577 individuals. Our working sample consists of all urban never married women aged 15 to 54 (1,076 individuals) and a subsample of urban ever married females aged 15-54 to whom the fertility module of the survey was administered (1,237 individuals). The fertility module was administered to only one randomly selected ever-married woman in each household.
[See Table 1]
As shown in Table 1, mean age of marriage for the ever married women was 18.5 , with wage workers in the private and public sectors having a higher than average age at marriage and non-participants and non-wage workers having lower than average age at marriage. On average, these ever-married women have 3.8 children, with public and private wage workers, as well as the unemployed having fewer children than average. The pattern for children less than seven is less clear, with non-wage workers having fewer of them than wage workers but no-participants having more of them. These patterns could well indicate an association between employment status, on the one hand, and the timing of marriage and fertility, on the other hand, or they could simply be due to the fact that differences in educational and other characteristics among women in different employment states account for their differences in age at marriage and in fertility. It will be up to the multivariate analysis to show us how fertility and timing of marriage affect employment choices.
Comparing the never-married and the ever-married subsamples, the statistics shown in Table 1 show that the never-married women are much younger than the ever-married women. The distribution by age group reveals that 44 percent of the never-married women are below the age of 20, compared to only 1.6 percent of the ever-married ones. Never-married women are also more educated, and have more educated parents.
Never married women are somewhat more likely to be active than ever-married women, with an overall activity rate of 29 percent compared to 21 percent. However, they are also much four times as likely to be unemployed, with a 12 percent of them being unemployed compared to 3 percent for ever-married women. Never married women who are employed however, are much more likely to be private sector wage workers, whereas employed ever-married women are more likely to be non-wage or public sector workers. These results suggest that public sector work and non-wage work may be much more accommodating to the domestic and child rearing responsibilities that come with marriage than is private sector employment. Again, these preliminary observations will need to be confirmed in the multivariate analysis.
Comparing the characteristics of women in different employment states within the never-married subsample, we find that among wage workers in the public and private sectors are older, suggesting an association between these work states and a delay in marriage. There is a sharp contrast in education, however, among never-married women working for wages in the private and public sectors. Never married female wage workers in the private sector are significantly less educated than average, whereas their counterparts in the public sector are significantly more educated. A similar pattern holds true for the education of their fathers. Private wage workers are also much more likely to have an inactive father than never-married women in any other employment state. Turning to the ever-married women subsample, we note that unemployed women are the youngest among them, and non-wage workers the oldest. Although public sector wage workers are still the most educated among them, the least educated are non-wage workers, followed by non-participants. Again, similar patterns holds for father’s education. Mother’s education is invariably very low among ever-married women, with private and public wage workers having the most educated mothers.
4. Estimation Results
In what follows, we present estimation results in the order laid out in the methodology section above. We start with the determinants of the timing of marriage, moving onto the determinants of fertility ending with the nested logit participation model.
First Stage: Estimation of the Age at First Marriage
As indicated above, we estimate a parametric duration model for the age at first marriage using a Gamma parametrization. The first thing to note is that the instrument we selected for the timing of marriage, namely the number of married sisters is highly significant and has the expected negative sign. Because parents with many daughters will typically want to marry them off quickly, women with more married sisters tend to marry earlier. The marginal effect indicates that each additional married sister reduces the age at marriage by about 0.6 years for the reference woman [6]. We marked the few cases that had missing information on married sisters with an indicator variable. The fact that this variable is positive and significant suggests that women with few or no married sisters were more likely to report the number of married sisters as missing.
[See Table 2]
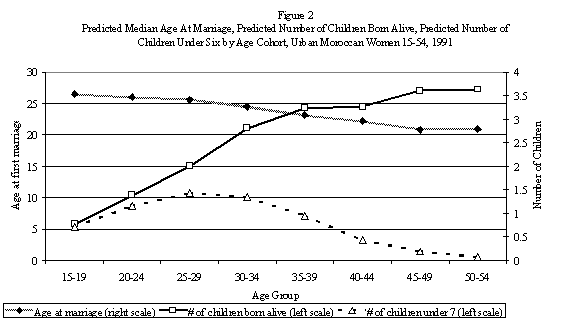
The fact that the coefficients of the age cohort dummies are all negative indicates that, as expected, age at marriage has increased steadily over the years in Morocco. As shown in Figure 2, women with reference characteristics above age 45 have the lowest predicted age at marriage of about 21 and the predicted age at marriage increases steadily as age declines to reach about 26 years for the youngest women in the sample.
As expected, a woman’s own education significantly raises the age at marriage. A woman with reference characteristics have has had some primary education marry 0.52 years later than one with no education, and one who completed more than six years of schooling marries 4.4 years later. Parental education also tends to raise women’s age of marriage, as educated parents are more likely to be aware of the problems associated with marrying their daughters early. A reference woman with a father who has some primary education marries 1.1 years later than one who’s father is illiterate, and one whose father has some secondary education or more marries 1.4 years later. Mother’s education has an even larger effect. A reference woman whose mother has some primary education marries 2.5 years later than one whose mother is illiterate. The fact there is no significant effect for mothers with higher levels of education can probably be attributed to the very small fraction of mothers with more than primary education.
It is hard to know a priori what direction of effect to expect on a father’s activity status. It turns out that active fathers marry their daughters much sooner than inactive fathers. Since paternal activity is probably related to the age of the father, this is probably an indication of the difference in age between father and daughter. Holding the woman’s age constant, an inactive father probably indicates an older father and therefore a larger age difference. Fathers who have daughters later in life are probably less likely to marry them off early. Maternal activity has the expected positive effect on age at marriage. Mothers who work are more likely to want to keep their daughters at home with them to help with household chores.
We decided to specify the regions of Morocco in this regression at a greater level of detail to capture possible cultural and ethnic differences in attitudes about early marriage. With the Casa Blanca region as the reference category, we note a somewhat lower age at marriage in the Southern region of Guelmime–Es Semara, in the Center-South region of Tadla-Azilal, in the Central region of Chaouia–Ouardigha, and in the Northern region of Tanger–Tetouan. Age at marriage for urban women in other regions of the country is not significantly different from Casa Blanca, when other variables are controlled for.
Second Stage: The Fertility Equation
In this stage of the analysis we estimate the number of children born alive and the number of children under seven years of age present in the household for urban ever-married women between the ages of 15 and 54. As shown in Table 3, the predicted median age at first marriage obtained from the first stage, has the expected negative effect on fertility. For the reference woman, a delay in marrying of one year significantly reduces the reference woman’s fertility by 0.04 children. The effect on number of children under seven is not significant.
[See Table 3]
At least some of the age-specific rates of contraceptive use at the province level by type of contraception appear to be significant determinants of fertility, indicating that they are appropriate instruments. For the modern methods of contraception, three of the age-specific utilization rates are significant determinants of the total number of children born alive, and two of the three have the expected negative sign. Only the utilization rate for women 45-49 is a significant determinant of the number of children under age seven. For the traditional methods, five of the age-specific utilization rates have a significant effect on the total number of children born alive, with four out of the five, having the expected sign. None of the traditional methods utilization rates have an effect on the number of children under seven.
To further test the performance of our instruments, we conducted a Wald test of
the joint significance of all the coefficients of the age-specific rates of
modern contraceptive use and found them to be jointly significant in both
models. A similar test for the
traditional methods also proved significant.
Finally, we replaced the age-specific rates with a single rate of modern
contraceptive use and one of traditional contraceptive use and found both to be
negative and significant determinant of fertility in both models. As expected, the number of children born
alive increases steadily with age, with all the age group dummies being
positive, significant, and progressively larger. As shown in Figure 2, the predicted number of children born alive
for the reference woman increases from 0.77 children at age 15 to 19 to 3.23
children for women aged 35-39, stabilizes, and then increases again for women
45 to 49 and 50 to 54. The predicted
number of children under 6 increases from 0.71 at age 15-19 to reach a peak of
1.43 at age 25-29, and then declines steadily to about 0 at age 50 to 54.
The education variable is specified in a little more detail in this model than in the age of marriage regression, with dummy variables indicating levels of educational attainment from incomplete primary to university. Illiterate is still the reference category. In the regression for the total number of children born alive, all the education coefficients are negative and increasing in magnitude, indicating an inverse relationship between education and fertility. For the regression of children under seven, the coefficients are all negative as well, but there is a weaker association between the number of children in this age group and the education level, because the younger women who are likely to have such children are also likely to be more educated. The marginal effects indicate that increasing the level of education for the reference woman from illiterate to lower secondary reduces the total number of children she is expected to have from 0.77 to 0.59 children, a reduction of 23 percent. A further increase in education and increasing it all the way to university reduces it to 0.39 children or 49 percent.
Once a woman’s own education is taken into account, parental education seems to have a weak and insignificant effect on a woman’s fertility. The presence of other adult women in the household appears to significantly increase the total number of children born alive, but to reduce the number of children under seven. The first effect can be interpreted to be the result of the reduced burden of child care when other care providers are available. It is not clear why the presence of alternative care givers would reduce the number of children under seven.
Compared to Casa Blanca, the reference region, urban areas in the regions of Tensift and the East have higher fertility rates. Fertility in the urban areas of other regions seems to be no different from that of Casa Blanca.
Third Stage: The Participation Decision
In this stage of the analysis we estimate a structural nested logit model of participation with the probability of marriage, the expected number of children under seven and the expected number of children 6 and over as endogenous regressors. As indicated in the methodology section, the expected number-of-children variables are specified here as unconditional on marriage by multiplying the predicted number of children conditional on having married by the probability of having married. The estimation results are shown in Table 4. The reference state is inactive in the first level, non-wage worker in the second level, and private wage worker in the third level. The interpretation of the coefficient estimates is therefore how the relevant variable affects log odds of being active vs. inactive in the first level, being a wage worker versus a non-wage worker in the second level, conditional on having chosen to be active in the first level, and being a public wage worker or being unemployment versus a private wage worker in the third level, conditional on having chosen wage work in the second level.
[See Table 4]
The predicted probability of marriage appears on its own and interacted with the number of children conditional on being married. The interpretation of the coefficients associated with this variable is therefore the effect of being married and not having children, a situation in which few women find themselves in Morocco. Being married with no children, has no significant effect on the choice to be active nor the choice to be a wage worker. It has a large positive effect on being employed for wages in the public sector. In other words, has a negative effect of being employed for wages in the private sector once the wage work path has been chosen. This is not surprising given that a woman’s domestic responsibility increase significantly with marriage, making it incompatible with the usually long hours of work required in private sector wage work.
Surprisingly the predicted number of children under the age of seven has an insignificant impact on the probability of being active, on the probability of being a wage worker once active, and on the probability of being unemployed or a public sector worker, once a wage worker. In fact, the expected negative effect of having young children on private wage work seems to have been already captured by the probability of marriage variable.
Having
children who are seven years of age and older has a negative effect on the
probability of being a wage worker, once active, confirming that non-wage work
is more compatible with child care than wage work. It has insignificant effects on the choice of being active and an
insignificant effect on the type of wage work one engages in.
The
preceding reveal that wage work in the private and public sectors have
extremely different implications for married and unmarried women. The public sector appears to be much more
hospitable to married women. It seems
fairly easy to continue working in the public sector after marriage, whereas
most private sector workers quit their jobs after marrying. Although Moroccan law in theory provides for
paid and unpaid maternity leaves in all sectors, these are often only respected
in the public sector. Mothers in that
sector can also benefit from child care services and can generally work
significantly shorter hours than in the private sector. In contrast, it appears to be very difficult
to be a mother in the private sector.
We now move to the discussion of the remaining regressors on the participation decision. The coefficients estimates are shown in Table 4. Age and age squared have predictable pattern on the probability of being active and on the probability of wage work once active. These probabilities first increase with age and then decline after a certain point. The negative coefficient of age and positive coefficient on age squared in the case of participation in the public sector (relative to the private sector) shows in no uncertain terms the effects of the dramatic slowdown in public sector hiring in Morocco in recent years and the resultant aging of the public sector work force.
The probability of being active seems to have a U-shaped relationship with education, with the highest levels reached for illiterates and university graduates and lowest for the lower secondary level. However, none of the education dummies are significant for this selection process. Education does not seem to strongly influence the choice of engaging in wage work versus non-wage work either, once the decision to be active has been made. In contrast, education has a very strong effect on the probability of joining the public sector relative to working for wages in the private sector, and on the probability of unemployment, also relative to wage work in the private sector. The strong similarity in the effect of education on unemployment and public sector work suggests that unemployment in Morocco is strongly concentrated among the more educated youths who in the past would have been hired by the public sector but whose opportunities in that sector have been strongly curtailed by attempts to reduce the growth of that sector. The private sector on the other hand seems to hire primarily less educated workers, providing few acceptable opportunities for the more educated. The relative drop in unemployment at the university level indicates that those most affected by the slowdown in public sector hiring are workers with intermediate levels of education.
Once a woman’s own education has been controlled for, the education of the father seems to have little effect on the decision to be active and that of being a wage worker. However, it significantly increases the probability of working in the public sector and of being unemployed, relative to working for wages in the private sector. This confirms again that women from relatively more privileged backgrounds tend to shun wage work in the private sector and have a strong preference for public sector work. When they are unable to get such work, they remain unemployed. The education of the mother does not have much of an effect on the participation decision.
The presence of men in the household, irrespective of their employment status, tends to have no significant effect on the participation decision, once the other determinants have been controlled for. The presence of adult women seems to increase the probability of wage work, but the effect is only significant at the 10 percent level. This is in line with expectations, since other adult women can serve as alternative caregivers and can reduce the burden of domestic work, allowing a woman to work outside the home.
5. Conclusion
Our analysis has allowed us to elucidate the causal relationship between the timing of marriage and fertility on the one hand, and between these two factors and a woman’s participation decision in urban Morocco, while overcoming the methodological difficulties associated with the mutual interdependence of these decisions. Through a judicious choice of instruments for the timing of marriage and fertility, we were able to estimate structural equations that provide estimates for the effect of fertility and marital status on the participation decision. We were also able to specify participation as a set of distinct employment states, offering significantly different opportunities for women to reconcile between market work and their domestic responsibilities.
Our findings indicate that marriage per se significantly reduces participation in private wage work, relative to public wage work. We also find that participation as a whole and in wage work relative to non-wage work is not strongly affected by marriage. The results also suggest that the presence of children under seven does not have a significant effect beyond that of marriage. Since the arrival of children is an anticipated event once a women gets married, its effect may already be included in the effect of marriage. The larger the number of children 6 and over a woman has, the less likely she is to participate in wage work.
With regards to the other determinants of participation, our work confirms previous results that indicate a strong positive relationship between education and participation in public sector work and in the probability of being unemployed. It suggests that the significant increase in unemployment among youth in Morocco in recent years is directly associated with the slowdown in public sector employment. Since the public sector hires primarily female workers with intermediate and higher levels of education, these are the workers that have the highest rates of unemployment. It appears however that university educated workers experience less unemployment than those with secondary schooling.
Endnotes:
* The authors wish to gratefully acknowledge the generous advice and valuable comments provided by Dennis Ahlburg, Paul Glewwe, Brian McCall, Djavad Salehi-Isfahani, and Insan Tunali. We also wish to thank El-Daw Suliman and Mohamed Dioudich for help in obtaining some of the data we needed. We have benefited from generous financial support from the Mellon Foundation, as part of the ERF-University of Minnesota project on Gender, Work and Family in the Middle East.
[1] In a subsequent study we intend to address the problem of the downward bias of reported standard errors when predicted regressors are present by bootstrapping all three stages of the model and reporting the bootstrap standard errors.
[2] See STATA reference manual, Volume 3, p. 353
[3] The large effect that the presence of preschool children has on participation has been noted by Nakamura and Nakamura (1992) and Zie (1997).
[4] We assume that the unemployed are either wage or salary workers who lost their jobs or young new entrants to the workforce who are primarily seeking wage employment. This allows us to specify unemployment as an option within the wage branch. Those seeking to set up their own enterprises are not likely to be a significant fraction of the unemployed in Morocco.
[5] In our case, all the explanatory variables refer to the individual’s or her household’s characteristics rather than to the alternatives she selects so that the same explanatory variables show up at all three stages. Since each potential alternative is specified as a separate observation in the nested logit model, it was necessary to re-specify all the explanatory variables as interactions between the original explanatory variables and the relevant alternatives at teach level, thus leading to different vectors of explanatory variables at each level.
[6] The reference woman is one for whom all dummy variables take on a value of 1 and whose continuous variables are set at the sample mean. For purposes of this regression, the reference woman is a 15 to 19 year old illiterate woman who has no married sisters and whose parents have not completed their primary education and are not economically active. She lives in the Greater Casa Blanca region.
Bibliography
Assaad, R. et El-Hamidi, F.
2002. “Female Labor Supply in Egypt:
Participation and Hours of Work”, in
Human Capital: Population
Economics In The Middle East. Ismail Sirageldin (Ed.). London: I.B. Tauris. (forthcoming)
Assaad, R. et El-Hamidi, F.
2001. "Is All Work the Same? A
Comparison of the Determinants of Female Participation and Hours of Work in
Various Employment States in Egypt", in The Economics of Women and Work in the Middle East and North
Africa. Mine Cinar (Ed.) Research
in Middle East Economics, Vol. 4. Greenwich, Conn.: JAI Press.
Becker, G. S. 1965. “A
Theorie of the Allocation of Time”, Economic
Journal, Vol. 75, pp. 493-517.
Bianchi, Suzanne M. et D.
Spain. 1986. American Women in Transition.
New York: Russel Sage Foundation.
Blundell, R. 1990.
“Evaluating Structural Microeconometric Models of Labor Supply”, Paper
presented at the Sixth World Congress of the Econometric Society, Barcelona”,
August.
Browning, M. 1992. “Children
and Household Economic Behavior”, Journal
of Economic Literature , Vol. 30, no. 3, September, pp. 1434-1475.
Dayioglu, M.1999. “Labor
Market Participation of Women in Turkey”, in Women’s Identities and Roles in the Course of Change: Central Asia,
East and Central Europe and Turkey, F.
Acar and A. Ayata (Eds.), Köln: Brill,
pp. 44 –73.
Di Tommaso, Maria L. 1999. “A Trivariate Model of Participation, Fertility
and Wages: the Italian Case”, Cambridge Journal of Economics, 23, pp. 623-640.
El Aynaoui, J. P. 1997. “Participation, Choix Occupationnel et Gains
sur le Marché du Travail Segmenté : Une Analyse Appliquée au cas du Maroc”, Document de travail, no. 18, Centre d’Economie du Développement,
Université Montesquieu-Bordeaux IV.
Espenshade, Thomas J. 1985. “Marriage Trends in America: Estimates,
Implications, and Underlying Causes”, Population and Development Review, 11, pp.
193-245.
Greene, William H. 2000. Econometric Analysis, Prentice Hall, 4ème édition, New York.
Heckman, James J. et Robert J. Willis. 1977. “A Beta-logistic Model for the Analysis
of Sequential Labor Force
Participation by Married Women”, Journal of Political Economy, vol. 85, no1, pp. 27-58.
Heckman, J. J. et MaCurdy, T. E. 1986. “Labor Econometrics”. In Handbook of
Econometrics, Vol. 3Z. Griliches et M. Intriligator (Eds.), ,
Elseiver Science, 1986, pp. 1917-1977.
Killingsworth, M.R. 1983. Labor Supply, Cambridge University Press.
Killingsworth, M.R et Heckman, J.J. 1986. “Female Labor Supply: A Survey”, in Handbook of Labor Economics,
Vol. 1, O. Ashenfelter and R.
Layard (Eds.), , pp. 103-204.
Mroz, T. A. 1987. “The Sensitivity of an Empirical Model of Married Women’s Hours of Work
to Economic and Statistical Assumptions”, Econometrica, 55 pp. 765-99.
Nakamura, A. et M. Nakamura. 1992. “The Econometrics of Female Labor Supply and
Children”, Econometric
Review, Vol. 11, no 1, pp. 1-71.
Rodgers, Willard et Arland Thornton. 1985. “Changing Patterns of First Marriage in the
United states”, Demography
22, pp. 265-279.
Rosenzweig, M. R. et Wolpin, K. I. 1980. “Life-Cycle Labour Supply and Fertility:Casual
Inferences from Household Models”, Journal of Political Economy, Vol. 88, no. 2.
Schultz, T. P., (Ed.). 1974. Economics of the Family. University of Chicago Press, Chicago.
Tansel, Aysit. 1994. “Wage Employment and Returns to Education for Men and Women in Turkey.” Economics of Education Review 13 (4): 305-320.
Tansel, Aysit 1996. “Self-Employment,
Wage Employment an Returns to Education for Urban Men and Women in
Turkey”. In Education and the Labor Market in Turkey, T. Bulutay (ed.). Ankara: State Institute of Statistics.
Tansel, Aysit. 1999.
“Public-Private Employment Choice: Wage
Differentials and Gender in Turkey”
Working Paper 9913, Economic Research Forum for the Arab Countries, Iran
and Turkey, Cairo, Egypt.
Tunali, Insan and Cem
Baslevent. 2001. “Estimation of Female Labor Supply Parameters When
Self-Employment is an Option”. Economics Department Working Papers, Koç
University, Istanbul, Turkey
Willis, R. J. 1973. “A New Approach to the Economic Theory of Fertility Behaviour », Journal of Political Economy, Vol. 81, pp. 14-64.
Xie, X. 1997. “Children and Female Labour Supply Behaviour”, Applied Economics, vol. 29, pp.
1303-1310.
Table 1: Descriptive Statistics for the Variables Used in the Analysis, Urban Moroccan Women, Ages 15-54, 1991
|
|
Never Married |
|
Ever Married |
||||||||||
|
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
Endogenous
Variables: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
age at marriage |
N/A. |
N/A. |
N/A. |
N/A. |
N/A. |
N/A. |
|
18.262 |
17.351 |
19.078 |
21.148 |
18.429 |
18.458 |
|
|
|
|
|
|
|
|
|
(3.354) |
(2.892) |
(4.233) |
(4.466) |
(3.852) |
(3.568) |
|
total number of children |
N/A. |
N/A. |
N/A. |
N/A. |
N/A. |
N/A. |
|
4.064 |
3.922 |
2.688 |
2.239 |
2.429 |
3.808 |
|
|
|
|
|
|
|
|
|
(2.784) |
(3.090) |
(1.983) |
(1.794) |
(3.128) |
(2.779) |
|
number of children under 7 |
N/A. |
N/A. |
N/A. |
N/A. |
N/A. |
N/A. |
|
0.888 |
0.558 |
0.719 |
0.648 |
0.571 |
0.833 |
|
|
|
|
|
|
|
|
|
(0.974) |
(0.925) |
(0.917) |
(0.774) |
(0.815) |
(0.956) |
|
Number of
Married Sisters: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
number of married sisters |
0.823 |
0.592 |
0.950 |
1.313 |
0.908 |
0.849 |
|
2.109 |
1.987 |
2.375 |
2.023 |
1.400 |
2.089 |
|
|
(1.314) |
(0.788) |
(1.329) |
(1.991) |
(1.235) |
(1.314) |
|
(1.672) |
(2.593) |
(2.059) |
(1.794) |
(1.439) |
(1.770) |
|
number of married sisters
missing |
0.058 |
0.082 |
0.188 |
0.094 |
0.108 |
0.078 |
|
0.013 |
0.039 |
0.031 |
0.057 |
0.086 |
0.021 |
|
|
(0.233) |
(0.277) |
(0.393) |
(0.296) |
(0.311) |
(0.268) |
|
(0.115) |
(0.195) |
(0.175) |
(0.233) |
(0.284) |
(0.144) |
|
Age and Age
Categories: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Age |
20.9 |
23.3 |
24.2 |
30.1 |
23.9 |
21.9 |
|
36.8 |
39.2 |
37.4 |
37.3 |
34.0 |
36.9 |
|
|
(5.7) |
(7.7) |
(7.4) |
(5.5) |
(4.7) |
(6.2) |
|
(9.6) |
(9.1) |
(7.8) |
(7.2) |
(10.5) |
(9.3) |
|
Age Squared |
466.9 |
603.4 |
642.3 |
937.3 |
591.2 |
518.6 |
|
1442.9 |
1617.8 |
1455.2 |
1445.4 |
1263.7 |
1449.5 |
|
|
(298.3) |
(446.9) |
(410.8) |
(344.6) |
(251.6) |
(329.1) |
|
(714.0) |
(692.8) |
(610.5) |
(558.6) |
(764.4) |
(700.2) |
|
Age 15-19* |
0.521 |
0.388 |
0.347 |
0.000 |
0.162 |
0.440 |
|
0.017 |
0.013 |
0.000 |
0.000 |
0.057 |
0.016 |
|
|
(0.500) |
(0.487) |
(0.476) |
(0.000) |
(0.368) |
(0.496) |
|
(0.131) |
(0.113) |
(0.000) |
(0.000) |
(0.232) |
(0.126) |
|
Age 20-24 |
0.275 |
0.306 |
0.198 |
0.188 |
0.423 |
0.284 |
|
0.098 |
0.052 |
0.016 |
0.011 |
0.114 |
0.085 |
|
|
(0.447) |
(0.466) |
(0.400) |
(0.397) |
(0.496) |
(0.451) |
|
(0.297) |
(0.223) |
(0.125) |
(0.107) |
(0.323) |
(0.279) |
|
Age 25-29 |
0.128 |
0.122 |
0.208 |
0.281 |
0.323 |
0.164 |
|
0.151 |
0.117 |
0.141 |
0.114 |
0.257 |
0.149 |
|
|
(0.335) |
(0.331) |
(0.408) |
(0.457) |
(0.469) |
(0.370) |
|
(0.358) |
(0.323) |
(0.350) |
(0.319) |
(0.443) |
(0.356) |
|
Age 30-34 |
0.043 |
0.061 |
0.158 |
0.313 |
0.077 |
0.067 |
|
0.174 |
0.130 |
0.219 |
0.295 |
0.200 |
0.183 |
|
|
(0.203) |
(0.242) |
(0.367) |
(0.471) |
(0.268) |
(0.250) |
|
(0.379) |
(0.338) |
(0.417) |
(0.459) |
(0.406) |
(0.387) |
|
Age 35-39 |
0.021 |
0.082 |
0.069 |
0.156 |
0.008 |
0.031 |
|
0.170 |
0.156 |
0.297 |
0.216 |
0.057 |
0.175 |
|
|
(0.143) |
(0.277) |
(0.255) |
(0.369) |
(0.088) |
(0.172) |
|
(0.375) |
(0.365) |
(0.460) |
(0.414) |
(0.236) |
(0.380) |
|
Age 40-44 |
0.007 |
0.020 |
0.010 |
0.063 |
0.000 |
0.008 |
|
0.138 |
0.195 |
0.141 |
0.182 |
0.086 |
0.143 |
|
|
(0.081) |
(0.143) |
(0.100) |
(0.246) |
(0.000) |
(0.091) |
|
(0.345) |
(0.399) |
(0.350) |
(0.388) |
(0.284) |
(0.350) |
Table 1: Descriptive Statistics (Continued)
|
|
Never Married |
|
Ever Married |
||||||||||
|
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
Age 45-49 |
0.003 |
0.000 |
0.000 |
0.000 |
0.008 |
0.003 |
|
0.122 |
0.208 |
0.063 |
0.114 |
0.114 |
0.124 |
|
|
(0.051) |
(0.000) |
(0.000) |
(0.000) |
(0.088) |
(0.053) |
|
(0.328) |
(0.408) |
(0.244) |
(0.319) |
(0.323) |
(0.329) |
|
Age 50-54 |
0.003 |
0.020 |
0.010 |
0.000 |
0.000 |
0.004 |
|
0.131 |
0.130 |
0.125 |
0.068 |
0.114 |
0.125 |
|
|
(0.051) |
(0.143) |
(0.100) |
(0.000) |
(0.000) |
(0.061) |
|
(0.337) |
(0.338) |
(0.333) |
(0.254) |
(0.323) |
(0.331) |
|
Own Schooling: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
no schooling* |
0.195 |
0.184 |
0.465 |
0.094 |
0.108 |
0.206 |
|
0.695 |
0.779 |
0.578 |
0.125 |
0.486 |
0.648 |
|
|
(0.396) |
(0.387) |
(0.499) |
(0.291) |
(0.310) |
(0.405) |
|
(0.461) |
(0.415) |
(0.494) |
(0.331) |
(0.500) |
(0.478) |
|
incomplete primary |
0.178 |
0.490 |
0.257 |
0.031 |
0.162 |
0.193 |
|
0.170 |
0.143 |
0.078 |
0.057 |
0.314 |
0.159 |
|
|
(0.383) |
(0.505) |
(0.439) |
(0.177) |
(0.369) |
(0.395) |
|
(0.375) |
(0.352) |
(0.270) |
(0.233) |
(0.471) |
(0.366) |
|
complete primary |
0.315 |
0.204 |
0.089 |
0.188 |
0.231 |
0.275 |
|
0.086 |
0.026 |
0.031 |
0.159 |
0.000 |
0.082 |
|
|
(0.465) |
(0.407) |
(0.286) |
(0.397) |
(0.423) |
(0.447) |
|
(0.281) |
(0.160) |
(0.175) |
(0.368) |
(0.000) |
(0.275) |
|
lower secondary |
0.229 |
0.061 |
0.099 |
0.250 |
0.200 |
0.206 |
|
0.032 |
0.026 |
0.109 |
0.205 |
0.057 |
0.049 |
|
|
(0.421) |
(0.242) |
(0.300) |
(0.440) |
(0.402) |
(0.405) |
|
(0.176) |
(0.160) |
(0.315) |
(0.406) |
(0.236) |
(0.215) |
|
vocational secondary |
0.016 |
0.041 |
0.069 |
0.156 |
0.115 |
0.038 |
|
0.009 |
0.000 |
0.063 |
0.216 |
0.057 |
0.027 |
|
|
(0.124) |
(0.200) |
(0.255) |
(0.369) |
(0.321) |
(0.192) |
|
(0.096) |
(0.000) |
(0.244) |
(0.414) |
(0.236) |
(0.164) |
|
upper secondary |
0.056 |
0.020 |
0.020 |
0.094 |
0.131 |
0.061 |
|
0.003 |
0.013 |
0.031 |
0.114 |
0.057 |
0.015 |
|
|
(0.231) |
(0.143) |
(0.140) |
(0.296) |
(0.338) |
(0.240) |
|
(0.055) |
(0.114) |
(0.175) |
(0.319) |
(0.236) |
(0.120) |
|
university |
0.010 |
0.000 |
0.000 |
0.188 |
0.054 |
0.020 |
|
0.005 |
0.013 |
0.109 |
0.125 |
0.029 |
0.020 |
|
|
(0.102) |
(0.000) |
(0.000) |
(0.397) |
(0.227) |
(0.138) |
|
(0.072) |
(0.114) |
(0.315) |
(0.333) |
(0.169) |
(0.141) |
|
Parental Schooling: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
father, illiterate or
incomp. primary* |
0.527 |
0.653 |
0.782 |
0.375 |
0.485 |
0.547 |
|
0.783 |
0.831 |
0.766 |
0.602 |
0.571 |
0.766 |
|
|
(0.499) |
(0.476) |
(0.413) |
(0.484) |
(0.500) |
(0.498) |
|
(0.412) |
(0.375) |
(0.424) |
(0.489) |
(0.495) |
(0.423) |
|
father, complete primary |
0.321 |
0.286 |
0.168 |
0.563 |
0.415 |
0.323 |
|
0.191 |
0.156 |
0.125 |
0.307 |
0.400 |
0.200 |
|
|
(0.467) |
(0.456) |
(0.376) |
(0.504) |
(0.495) |
(0.468) |
|
(0.393) |
(0.365) |
(0.333) |
(0.464) |
(0.497) |
(0.400) |
|
father, secondary or above |
0.152 |
0.061 |
0.050 |
0.063 |
0.100 |
0.129 |
|
0.026 |
0.013 |
0.109 |
0.091 |
0.029 |
0.034 |
|
|
(0.359) |
(0.242) |
(0.218) |
(0.246) |
(0.301) |
(0.336) |
|
(0.158) |
(0.114) |
(0.315) |
(0.289) |
(0.169) |
(0.181) |
|
mother, illiterate or
incomp, primary* |
0.822 |
0.878 |
0.931 |
0.938 |
0.831 |
0.839 |
|
0.980 |
0.974 |
0.922 |
0.943 |
0.971 |
0.974 |
|
|
(0.383) |
(0.328) |
(0.254) |
(0.242) |
(0.375) |
(0.367) |
|
(0.138) |
(0.159) |
(0.268) |
(0.231) |
(0.167) |
(0.159) |
|
mother, complete primary |
0.115 |
0.102 |
0.040 |
0.031 |
0.138 |
0.108 |
|
0.014 |
0.013 |
0.031 |
0.034 |
0.000 |
0.016 |
|
|
(0.319) |
(0.306) |
(0.196) |
(0.177) |
(0.347) |
(0.310) |
|
(0.119) |
(0.114) |
(0.175) |
(0.183) |
(0.000) |
(0.126) |
Table 1: Descriptive Statistics (Continued)
|
|
Never Married |
|
Ever Married |
||||||||||
|
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
mother, secondary or above |
0.063 |
0.020 |
0.030 |
0.031 |
0.031 |
0.053 |
|
0.005 |
0.013 |
0.047 |
0.023 |
0.029 |
0.010 |
|
|
(0.243) |
(0.143) |
(0.171) |
(0.177) |
(0.173) |
(0.224) |
|
(0.072) |
(0.114) |
(0.213) |
(0.150) |
(0.169) |
(0.098) |
|
Parental Activity Status: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
father, active |
0.827 |
0.898 |
0.931 |
0.719 |
0.777 |
0.831 |
|
0.989 |
0.961 |
1.000 |
0.943 |
0.943 |
0.983 |
|
|
(0.378) |
(0.306) |
(0.255) |
(0.457) |
(0.418) |
(0.375) |
|
(0.106) |
(0.195) |
(0.000) |
(0.233) |
(0.236) |
(0.129) |
|
mother, active |
0.139 |
0.265 |
0.178 |
0.094 |
0.138 |
0.147 |
|
0.111 |
0.195 |
0.188 |
0.080 |
0.143 |
0.119 |
|
|
(0.346) |
(0.446) |
(0.385) |
(0.296) |
(0.347) |
(0.354) |
|
(0.314) |
(0.399) |
(0.393) |
(0.272) |
(0.355) |
(0.324) |
|
Household Characteristics: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
presence of inactive males |
0.559 |
0.408 |
0.356 |
0.594 |
0.469 |
0.523 |
|
0.398 |
0.260 |
0.172 |
0.239 |
0.314 |
0.364 |
|
|
(0.813) |
(0.840) |
(0.687) |
(0.798) |
(0.864) |
(0.811) |
|
(0.731) |
(0.616) |
(0.521) |
(0.479) |
(0.932) |
(0.708) |
|
presence of male wage
workers |
0.429 |
0.469 |
0.436 |
0.250 |
0.300 |
0.411 |
|
0.365 |
0.416 |
0.203 |
0.125 |
0.200 |
0.338 |
|
|
(0.750) |
(0.767) |
(0.767) |
(0.568) |
(0.643) |
(0.736) |
|
(0.644) |
(0.695) |
(0.596) |
(0.396) |
(0.473) |
(0.630) |
|
presence of male non-wage
workers |
0.359 |
0.327 |
0.267 |
0.156 |
0.231 |
0.327 |
|
0.342 |
0.234 |
0.281 |
0.136 |
0.286 |
0.316 |
|
|
(0.696) |
(0.555) |
(0.527) |
(0.574) |
(0.536) |
(0.656) |
|
(0.629) |
(0.535) |
(0.487) |
(0.345) |
(0.572) |
(0.602) |
|
presence of other adult
females |
0.988 |
0.939 |
0.970 |
0.906 |
0.962 |
0.979 |
|
0.576 |
0.714 |
0.500 |
0.568 |
0.543 |
0.579 |
|
|
(0.108) |
(0.242) |
(0.171) |
(0.296) |
(0.193) |
(0.145) |
|
(0.495) |
(0.455) |
(0.504) |
(0.498) |
(0.505) |
(0.494) |
|
Modern contraceptive use in province: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
by women 15-19 |
0.308 |
0.286 |
0.337 |
0.276 |
0.268 |
0.304 |
|
0.300 |
0.267 |
0.367 |
0.281 |
0.277 |
0.299 |
|
|
(0.217) |
(0.243) |
(0.298) |
(0.220) |
(0.198) |
(0.225) |
|
(0.213) |
(0.218) |
(0.298) |
(0.261) |
(0.191) |
(0.222) |
|
by women 20-24 |
0.340 |
0.373 |
0.393 |
0.395 |
0.338 |
0.348 |
|
0.340 |
0.341 |
0.384 |
0.369 |
0.327 |
0.344 |
|
|
(0.133) |
(0.201) |
(0.143) |
(0.224) |
(0.111) |
(0.140) |
|
(0.141) |
(0.192) |
(0.146) |
(0.161) |
(0.135) |
(0.147) |
|
by women 25-29 |
0.419 |
0.431 |
0.427 |
0.433 |
0.420 |
0.421 |
|
0.418 |
0.427 |
0.414 |
0.428 |
0.404 |
0.418 |
|
|
(0.121) |
(0.110) |
(0.121) |
(0.118) |
(0.132) |
(0.121) |
|
(0.117) |
(0.113) |
(0.136) |
(0.132) |
(0.121) |
(0.119) |
|
by women 30-34 |
0.430 |
0.414 |
0.441 |
0.370 |
0.434 |
0.429 |
|
0.420 |
0.398 |
0.419 |
0.442 |
0.408 |
0.420 |
|
|
(0.135) |
(0.170) |
(0.157) |
(0.174) |
(0.128) |
(0.140) |
|
(0.138) |
(0.170) |
(0.161) |
(0.166) |
(0.137) |
(0.143) |
|
by women 35-39 |
0.467 |
0.470 |
0.436 |
0.456 |
0.446 |
0.462 |
|
0.475 |
0.463 |
0.442 |
0.454 |
0.429 |
0.470 |
|
|
(0.135) |
(0.108) |
(0.120) |
(0.133) |
(0.128) |
(0.132) |
|
(0.148) |
(0.147) |
(0.139) |
(0.135) |
(0.115) |
(0.146) |
|
by women 40-44 |
0.406 |
0.410 |
0.384 |
0.433 |
0.423 |
0.407 |
|
0.412 |
0.448 |
0.383 |
0.388 |
0.424 |
0.411 |
|
|
(0.148) |
(0.199) |
(0.172) |
(0.167) |
(0.174) |
(0.157) |
|
(0.167) |
(0.201) |
(0.190) |
(0.190) |
(0.218) |
(0.174) |
|
by women 45-49 |
0.263 |
0.269 |
0.275 |
0.272 |
0.289 |
0.268 |
|
0.246 |
0.250 |
0.247 |
0.268 |
0.277 |
0.249 |
|
|
(0.148) |
(0.177) |
(0.162) |
(0.153) |
(0.152) |
(0.151) |
|
(0.157) |
(0.196) |
(0.177) |
(0.153) |
(0.203) |
(0.162) |
Table 1: Descriptive Statistics (Continued)
|
|
Never Married |
|
Ever Married |
||||||||||
|
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
Inactive |
Non-Wage Workers |
Private Wage Workers |
Public Wage Worker |
Unemployed |
All |
|
Traditional contraceptive use in province: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
by women 15-19 |
0.004 |
0.000 |
0.013 |
0.000 |
0.003 |
0.004 |
|
0.003 |
0.001 |
0.005 |
0.015 |
0.010 |
0.004 |
|
|
(0.034) |
(0.002) |
(0.065) |
(0.000) |
(0.029) |
(0.036) |
|
(0.030) |
(0.003) |
(0.042) |
(0.070) |
(0.056) |
(0.035) |
|
by women 20-24 |
0.043 |
0.034 |
0.044 |
0.052 |
0.043 |
0.043 |
|
0.041 |
0.034 |
0.031 |
0.041 |
0.036 |
0.040 |
|
|
(0.047) |
(0.048) |
(0.049) |
(0.050) |
(0.045) |
(0.047) |
|
(0.046) |
(0.052) |
(0.042) |
(0.050) |
(0.046) |
(0.046) |
|
by women 25-29 |
0.042 |
0.031 |
0.040 |
0.051 |
0.044 |
0.042 |
|
0.039 |
0.028 |
0.026 |
0.047 |
0.030 |
0.038 |
|
|
(0.046) |
(0.045) |
(0.058) |
(0.051) |
(0.051) |
(0.048) |
|
(0.045) |
(0.040) |
(0.044) |
(0.062) |
(0.040) |
(0.046) |
|
by women 30-34 |
0.063 |
0.060 |
0.071 |
0.051 |
0.069 |
0.064 |
|
0.064 |
0.064 |
0.067 |
0.079 |
0.056 |
0.065 |
|
|
(0.054) |
(0.055) |
(0.054) |
(0.039) |
(0.057) |
(0.054) |
|
(0.059) |
(0.050) |
(0.056) |
(0.058) |
(0.042) |
(0.058) |
|
by women 35-39 |
0.081 |
0.066 |
0.098 |
0.076 |
0.081 |
0.082 |
|
0.081 |
0.077 |
0.073 |
0.096 |
0.073 |
0.081 |
|
|
(0.066) |
(0.072) |
(0.082) |
(0.080) |
(0.070) |
(0.069) |
|
(0.067) |
(0.067) |
(0.075) |
(0.083) |
(0.066) |
(0.069) |
|
by women 40-44 |
0.064 |
0.067 |
0.099 |
0.095 |
0.074 |
0.069 |
|
0.060 |
0.057 |
0.071 |
0.109 |
0.064 |
0.064 |
|
|
(0.087) |
(0.091) |
(0.107) |
(0.098) |
(0.090) |
(0.090) |
|
(0.085) |
(0.080) |
(0.082) |
(0.117) |
(0.081) |
(0.088) |
|
by women 45-49 |
0.067 |
0.073 |
0.095 |
0.049 |
0.062 |
0.069 |
|
0.064 |
0.057 |
0.081 |
0.090 |
0.052 |
0.066 |
|
|
(0.077) |
(0.085) |
(0.077) |
(0.064) |
(0.067) |
(0.077) |
|
(0.078) |
(0.071) |
(0.083) |
(0.077) |
(0.059) |
(0.078) |
|
Region: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
South |
0.110 |
0.122 |
0.129 |
0.219 |
0.085 |
0.112 |
|
0.132 |
0.169 |
0.250 |
0.080 |
0.200 |
0.138 |
|
|
(0.313) |
(0.331) |
(0.337) |
(0.420) |
(0.279) |
(0.316) |
|
(0.338) |
(0.377) |
(0.436) |
(0.272) |
(0.406) |
(0.345) |
|
Tensift |
0.149 |
0.204 |
0.198 |
0.313 |
0.223 |
0.170 |
|
0.131 |
0.182 |
0.156 |
0.205 |
0.171 |
0.141 |
|
|
(0.357) |
(0.407) |
(0.400) |
(0.471) |
(0.418) |
(0.376) |
|
(0.337) |
(0.388) |
(0.366) |
(0.406) |
(0.382) |
(0.349) |
|
Center* |
0.101 |
0.143 |
0.218 |
0.094 |
0.115 |
0.115 |
|
0.117 |
0.182 |
0.188 |
0.102 |
0.257 |
0.128 |
|
|
(0.301) |
(0.350) |
(0.413) |
(0.291) |
(0.319) |
(0.319) |
|
(0.322) |
(0.386) |
(0.390) |
(0.303) |
(0.437) |
(0.334) |
|
North-West |
0.154 |
0.163 |
0.218 |
0.125 |
0.215 |
0.167 |
|
0.140 |
0.169 |
0.109 |
0.284 |
0.171 |
0.151 |
|
|
(0.362) |
(0.373) |
(0.415) |
(0.336) |
(0.413) |
(0.373) |
|
(0.347) |
(0.377) |
(0.315) |
(0.454) |
(0.382) |
(0.358) |
|
Center-North |
0.134 |
0.122 |
0.178 |
0.094 |
0.108 |
0.133 |
|
0.148 |
0.169 |
0.188 |
0.159 |
0.143 |
0.152 |
|
|
(0.340) |
(0.331) |
(0.385) |
(0.296) |
(0.311) |
(0.340) |
|
(0.355) |
(0.377) |
(0.393) |
(0.368) |
(0.355) |
(0.359) |
|
East |
0.198 |
0.102 |
0.020 |
0.125 |
0.154 |
0.169 |
|
0.171 |
0.026 |
0.016 |
0.057 |
0.029 |
0.141 |
|
|
(0.398) |
(0.306) |
(0.140) |
(0.336) |
(0.362) |
(0.375) |
|
(0.376) |
(0.160) |
(0.125) |
(0.233) |
(0.169) |
(0.349) |
|
Center-South |
0.154 |
0.143 |
0.040 |
0.031 |
0.100 |
0.133 |
|
0.162 |
0.104 |
0.094 |
0.114 |
0.029 |
0.148 |
|
|
(0.362) |
(0.354) |
(0.196) |
(0.177) |
(0.301) |
(0.340) |
|
(0.369) |
(0.307) |
(0.294) |
(0.319) |
(0.169) |
(0.355) |
|
Number of Observations |
764 |
49 |
101 |
32 |
130 |
1076 |
|
973 |
77 |
64 |
88 |
35 |
1237 |
Standard Deviations are in parentheses.
* denotes reference category, N/A. = "not applicable"